Doubling the Cube Volume
A cube with an original side length (S1) of 5 units and corresponding volume (V1) of 125 cubic units has a new side length (S2) of 6.3 units when the volume is doubled (V2) to 250 cubic units.
*Answers rounded to three decimal places
Doubling the Cube Formula for Side
The cube doubling problems refers to doubling the volume of the cube. When the volume of the cube doubles at what rate does the side length increase? The formula below is used to calculate the side length of a doubled cube given an original cube with known side length:
- S2 = S1 x ∛2
Substitute the formula for doubled side length in to the formula for cube volume to directly find the volume of a cube (V2) with twice the volume (V1) of the original cube.
- V2 = (S1 x ∛2)3
What about finding the side length of the doubled cube if you only know the volume of the original cube? Recall the formula for finding the side length of the cube from the volume (S = ∛V) and substitute.
- V2 = (∛V1 x ∛2)3
Although we can solve this problem via the use of modern computational techniques it is known as one of the great epic problems in mathematics. Using the classical mathematical tools, a compass and a straight edge, the number ∛2 could not be constructed, therefore the problem was rendered unsolvable. Read more about the challenges of doubling the cube.
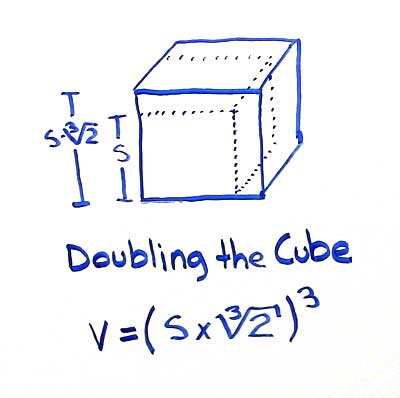
Given an original cube with a side length S1 the side length S2 of a cube with twice the volume can be found by multiplying the original side length by ∛2.
