Cube Space Diagonal
A cube with a side length (S) of 4 has a maximum diagonal line length through the space (volume) (L) of 6.9282.
Cube Space Diagonal Formula
for cubes the maximum length of a diagonal line through the interior space (volume) L and a side length S
- L = S√3
substitute the side length S with the measured value, in this example lets use a side length of 4
- L = 4√3
now use the square root function on your calculator to find the square root of 3 then multiply your answer by the side length of 4
- L = 5.769
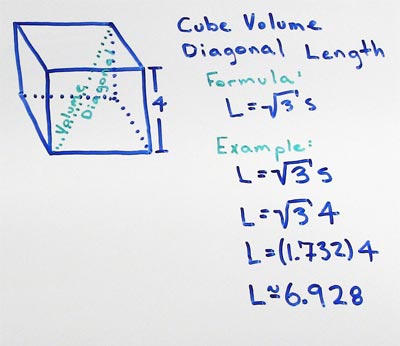
The maximum length (L) of a diagonal through a cube travels from one vertex to the opposite vertex across the empty space of the interior of the cube. It is calculated by multiplying the measured side length (S) of the cube by the square root of 3 (√3).
